Abstract
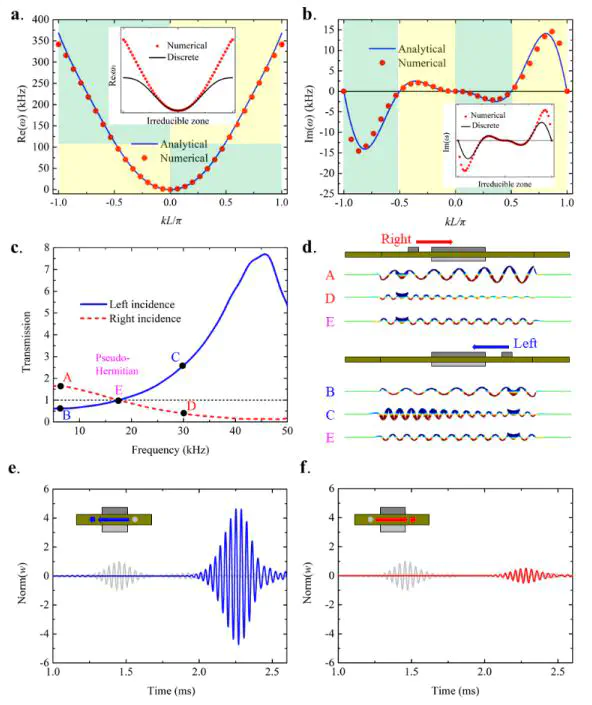
Active control schemes provide emergent wave properties and flexible tunability in mechanical systems. Here, we propose both analytically and numerically a non-Hermitian metamaterial system enabled by piezoelectric patches and electronic non-local feedback control. The metamaterial system is physically realized by a non-local microploar beam with non-local feedback control. Since the non-local feedback control breaks spatial reciprocity, the proposed metabeam supports not only non-reciprocal flexural wave amplification and attenuation, but also non-Hermitian skin effect featuring bulk localized eigenmodes in the finite structure. The non-reciprocal amplification and attenuation phenomena are quantitatively predicted by band structure analyses under both the continuum and discrete spring-mass representation, which can be attributed to the work exchange between mechanical and electric works. The non-Hermitian skin effect and the associated bulk localized eigenmodes are characterized by a topological invariant. In addition, direction-dependent bending stiffness is also demonstrated in the non-local micropolar piezoelectric metabeam with proper transfer functions. The electronically controllable non-Hermitian metabeam could pave the ways for designing future systems such as synthetic biofilaments and membranes with feed-back control schemes.
Supplementary notes can be added here, including code, math, and images.
Qian Wu (吳謙)
Postdoctoral Fellow of Mechanical Engineering
My research interests include active elastic metamaterials, topological mechanics and elastodynamics, and non-Hermitian elastic systems.