Abstract
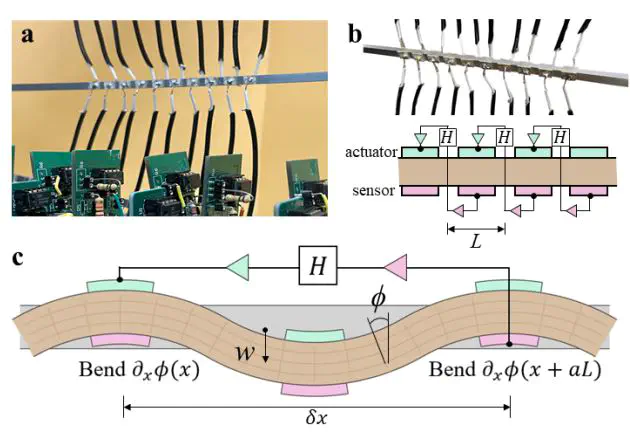
Active metamaterials with electronic control schemes can exhibit nonreciprocal and/or complex elastic coefficients that result in non-Hermitian wave phenomena. Here, we investigate theoretically and experimentally a non-Hermitian micropolar metabeam with piezoelectric elements and electronic nonlocal feed-forward control. Since the nonlocal feed-forward control breaks spatial reciprocity, the proposed metabeam supports nonreciprocal flexural wave propagation, featuring unidirectional amplification/attenuation and non-Hermitian skin effect. Theoretical homogenization modeling is developed to consider the nonlocal effect into an effective complex bending stiffness. The unidirectional wave amplification/attenuation is attributed to the energy conversion between electrical power and mechanical work. The non-Hermitian skin effect, characterized by a winding number, is the manifestation of the flexural nonreciprocity and admits an extensive number of localized bulk eigenmodes on open boundaries. The nonlocal metabeam is also employed to engineer the anomalous wave dispersion such as tunable roton-like dispersion and band tilting. Its reciprocity can be easily maintained or broken through electrically programmable transfer functions. The nonlocal micropolar metabeam could pave the ways for designing non-Hermitian topological mechanical metamaterials featuring programmable nonreciprocal wave transmission and engineering roton-like wave dispersion relations under ambient environments.
Supplementary notes can be added here, including code, math, and images.
Qian Wu (吳謙)
Postdoctoral Fellow of Mechanical Engineering
My research interests include active elastic metamaterials, topological mechanics and elastodynamics, and non-Hermitian elastic systems.