In-Plane Second-Order Topologically Protected States in Elastic Kagome Lattices

Abstract

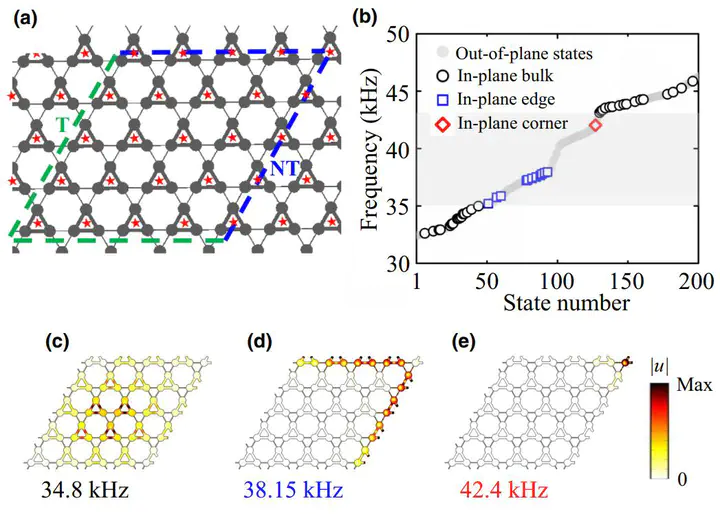
Second-order topological insulators, which exhibit capability of hosting topologically protected zero-dimensional corner states distinct from the well-studied topological edge states, unveil a horizon beyond the conventional bulk-edge correspondence. Motivated by recent experimental observation of Wannier-type second-order corner states in acoustic structures, we investigate numerically and demonstrate experimentally the in-plane edge and corner states in a mechanical kagome lattice. By manipulating simply lattice geometry and quantized characterization, we exploit that the emerging corner states are topologically robust against disorders. We further present a second-order topological insulator with multi-interfaces such that the mechanical energy can be localized in multiple locations, which provides the possibility of practical application in energy harvesting devices. The present study is the physical observation to extend the second-order topological insulator to in-plane elastic dynamics, and modal coupling of in-plane elasticity makes it more challenging to be measured experimentally.

Qian Wu (吳謙)

Postdoctoral Fellow of Mechanical Engineering

My research interests include active elastic metamaterials, topological mechanics and elastodynamics, and non-Hermitian elastic systems.